Question

Can someone please explain how to find this answer? thanks

Answer 1

so, a line that is parallel to 5x-2y = -12, will have the same exact slope as that equation's, so what is it anyway?


`\bf 5x-2y=-12\implies 5x+12=2y\implies \cfrac{5x+12}{2}=y \\\\\\ \cfrac{5x}{2}+\cfrac{12}{2}=y\implies \stackrel{slope}{\cfrac{5}{2}}x+6=y`

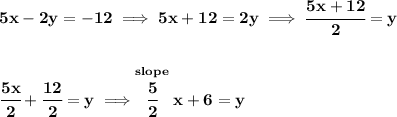
so, notice, from the slope-intercept form, it happens that the slope is 5/2, well, the line will have the same slope.

so we're looking for the equation of a line whose slope is 5/2 and runs through -2,3


`\bf \begin{array}{ccccccccc} &&x_1&&y_1\\ &&(~ -2 &,& 3~) \end{array} \\\\\\ % slope = m slope = m\implies \cfrac{5}{2} \\\\\\ % point-slope intercept \stackrel{\textit{point-slope form}}{y- y_1= m(x- x_1)}\implies y-3=\cfrac{5}{2}[x-(-2)] \\\\\\ y-3=\cfrac{5}{2}(x+2)\implies y-3=\cfrac{5}{2}x+5\implies y=\cfrac{5}{2}x+8`

Answer 2

I would start with the standard form equation of the parallel line.
.. 5x -2y = 5(-2) -2(3) = -16
Then solve for y.
.. 2y = 5x +16 . . . add 2y+16; then divide by 2 for the next equation
.. y = (5/2)x +8 . . . . . . . corresponds to selection (B)