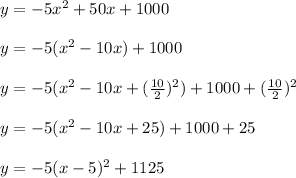Question

Help please! Math Nation Section 6 Test Yourself Practice Tool.

Answer 1

Based on the table of values, an equation of the quadratic that models the data is: D.
`y = -5(x-5 ) ^2+ 1125`

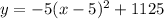
In Mathematics and Euclidean Geometry, the vertex form of a quadratic function is represented by the following mathematical equation:

`y = a(x - h)^2 + k`

Where:

• h and k represents the vertex of the graph.
• a represents the leading coefficient.

In order to determine an equation for the line of best fit or quadratic regression line that models the data points contained in the table of values, we would have to use a graphing calculator (Microsoft Excel).

Based on the scatter plot (see attachment) which models the relationship between the number of $2 increase in price (in dollars), x and revenue, y, the quadratic regression is given by:

`y =-5x^2 + 50x + 1000\\\\y = -5(x^2 - 10x) + 1000\\\\y = -5(x^2 - 10x + ((10)/(2))^2 ) + 1000+ ((10)/(2))^2\\\\y = -5(x^2 - 10x + 25 ) + 1000+25\\\\y = -5(x-5 ) ^2+ 1125`

Answer 2

Answer: D)
`y=-5(x-5)^2+1125`

Explanation:

Let x be the number of $2 increases in price and y be the revenue.

By using the given table , lets check all the options

A)
`y=(x+5)^2-1125`

For x=1, y=1045

`y=(1+5)^2-1125=36-1125=-1089\\\\But\ 1045\\eq-1089`

B)
`y=(x-5)^2+1125`

For x=1, y=1045

`y=(1-5)^2+1125=14+1125=1139\\\But\ 1045\\eq1139`

C)
`y=-5(x+5)^2-1125`

`y=-5(1+5)^2-1125=-5(36)-1125=-1305\\\\But\ 1045\\eq-1305`

D)
`y=-5(x-5)^2+1125`

`y=-5(1-5)^2+1125=-5(16)+1125=1045`

Hence, this is the quadratic equation that models the data.