Answer:
Let x represent the number of blueberry muffins
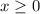
Let y represent the number of bran muffins

Tray of blueberry muffins: 1/3 cup of oil & 2 eggs
Tray of bran muffins: 1/2 cup of oil & 1 egg
Alan has 4 cups of oil and 12 eggs on hand.
He sells a tray of blueberry muffins for $12 each.
He sells a tray of bran muffins for $9 each.

The constraints for the problem are 4 cups of oil and 12 eggs.
Alan should not exceed 4 cups of oil and 12 eggs as it will create shortage. He should get the correct proportion of both the muffins to maximize his profit.
In equation form it is :
