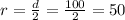Question

Given a circle with measures of (C, d, and r) and a circle with measures of (C', d', and r'), what is r if C C' = 5 and d' = 20?

Answer 1

r = 50

Explanation:

We know that:

• 
  `(C)/(C')=5`
• 
  `d'=20`

So, the ratio between the circumferences is 4 and the diameter of the second circle is 20. In this case, we have to use the ratio between those two circumferences, because that's what is our given data.

`(C)/(C')=(d)/(d')\\5=(d)/(20)\\ 100=d`

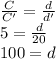
From this proportion, we deduct that the diameter of the initial circle is 100. Now, we know that the radius in a circumference is have the diameter. Therefore, the radius is:

`r=(d)/(2)=(100)/(2)=50`