Question

The number of diagonals in any polygon is whole number. But on the other side the formula of the number of diagonals in any convex polygon is in a fraction form  \frac{n(n-3)}{2[tex] . How can you explain this?

Answer 1

I think the formula for the number of diagonals of a convex polygon is actually

`N=n(n-1)/2`
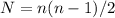
This will always give a result of a whole number because
if n is odd, then n-1 is even, or
if n is even, n-1 must be odd.
So the division by 2 will always give a whole number because there is always an even number in the numerator.

By the way, this number is also solution to the "hand-shake" problem, which is "how many possible handshakes in a group of n people, if everyone shakes hand with everyone else exactly once?" Therefore, again, it is a whole number.

Answer 2

you can explain this by doing n-3 times 2