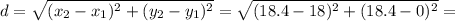Question

Two straight roads diverge at an angle of 45°. two cars leave the intersection at 2:00 p.m., one traveling at 36 mi/h and the other at 52 mi/h. how far apart are the cars at 2:30 p.m.?

Answer 1

Let's take the x-axis as the direction of car 1, which is traveling at speed
`v_1 = 36 mi/h`. Car 2 is traveling at speed
`v_2 = 52 mi/h` in a direction of
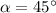
`\alpha = 45 ^(\circ)` with respect to the x-axis.

Let's start by finding the distance covered by the two cars in between 2.00 pm and 2.30 pm, so in 30 minutes. We can write 30 minutes as 0.5 hours, so
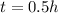
`t=0.5 h`. The distance covered by the two cars is

`S_1 = v_1 t = (36 mi/h)(0.5 h)= 18 mi`

`S_2 = v_2 t =(52 mi/h)(0.5 h)=26 mi`
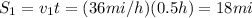
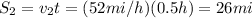
S1 lies on the x-axis, while we have to decompose S2 on both axes:

`S_(2x)=S_2 \cos \alpha = (26 mi)(\cos 45^(\circ))=18.4 mi`

`S_(2y)=S_2 \sin \alpha = (26 mi)(\sin 45^(\circ))=18.4 mi`

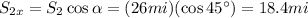
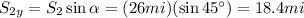
Assuming the two cars started their motion from the origin of the axes (0,0), then we can rewrite the final coordinates of the two cars as
- car 1: (18 mi,0)
- car 2: (18.4 mi, 18.4 mi)
And so the distance between the two cars will be

`d= √((x_2-x_1)^2+(y_2-y_1)^2)= √((18.4-18)^2+(18.4-0)^2)=`

`=18.4 mi`