Definition of luminosity is the total amount of energy emitted by the star per unit of time. We can use following formula to calculate the luminosity:
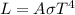
Where A is the surface area of the star.
We also have a very important mass-luminosity relationship:
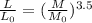
This formula gives us relationship between stars mass and it's luminosity.
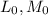
stands for Sun's luminosity and mass.
We can rewrite the luminosity formula like this:
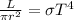
Now if we divide this by the Sun's luminosity we get:
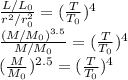
We can use this formula to estimate the mass. Surface temperature of the Sun is
5778 K.
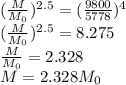
The answer would be 2 solar masses.