Question

Find the surface area and volume please hello with

Answer 1

First, let's consider what information we have.

We are given a right circular cone with a radius of 10 km and a diagonal of 22.4 km.

There are two formulae that we need: one for its volume and one for its surface area.

The volume of a cone is
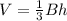`V = (1)/(3)Bh`, where B is the area of the base and h is the height. The base of a cone is a circle, so we use the area of a circle,
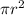`\pi r^2`, to get
`V =(1)/(3)\pi r^2h`.

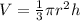We aren’t given the height explicitly; however, using the Pythagorean Theorem, we can find it. Treat the diagonal as the hypotenuse of a right triangle and the radius as a leg. We have

`(22.4)^2-10^2=h^2\\h = 20.0`.

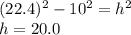Now, we can substitute our values into the formula for volume.

`V= (1)/(3) \pi r^2h = (1)/(3) \pi (10)^2(20)= (2000 \pi )/(3)=2094 \ km^3`

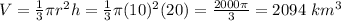
For the surface area, we have the formula
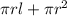`\pi rl+ \pi r^2`, where l is the diagonal that we had in the beginning.

So, we simply write
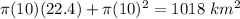`\pi (10)(22.4)+ \pi (10)^2=1018 \ km^2`.