Question

A satellite of mass 5420 kg orbits the earth and has a period of 6560 s.determine the radius of its circular orbit.

Answer 1

The satellite is in circular motion, and the only force acting on it is the gravity exerted from the Earth:

`F=G (Mm)/(r^2)`
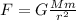
where
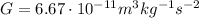
`G=6.67 \cdot 10^(-11)m^3 kg^(-1)s^(-2)` is the gravitational constant,
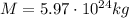
`M=5.97 \cdot 10^(24)kg` is the Earth's mass, m is the mass of the satellite and r is the radius of the circular orbit.
Since it is a circular motion, this force acts as centripetal force,
`m (v^2)/(r)`:

`m (v^2)/(r) =G (Mm)/(r^2)`
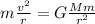
where v is the satellite's speed.

But the speed is also equal to the distance covered in one revolution (which is the circumference:
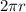
`2 \pi r`) divided by the time needed to cover one revolution (which is the period T=6560 s):

`v= (2 \pi r)/(T)`

By replacing this into the previous formula and simplifying ,we get

`(4 \pi^2 r)/(T^2) = (GM)/(r^2)`

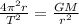
And re-arranging and substituting the values, we find the radius of the orbit:

`r= \sqrt[3]{ (T^2 G M)/(4 \pi^2) } = 7.57 \cdot 10^7 m=7570 km`