Question

The figures below are made out of circles, semicircles, quarter circles, and a square. Find the area and the perimeter of each figure and give your answers as a completely simplified exact value in terms of π (no approximations).

Answer 1

A=16(pi-2),p=4(2 sqrt2+pi)

Explanation:

Answer 2

I. ABCD is a square so ∡BCD=90°
|BC|²+|CD|² = |BD|²
8² + 8² = |BD|²
|BD|² = 8²·2
|BD| = √[8²·2]
|BD| = 8√2

II. Circular segment BCD is a quater of circle (because ∡BCD=90°)
R=8

So the lenght of arc BD:
`L_(BD)=\frac14\cdot 2\pi\cdot R = \frac12\cdot\pi\cdot8 = 4\pi`

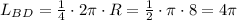Perimeter of the figure: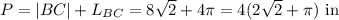

`P=|BC|+L_(BC) = 8\sqrt2+4\pi = 4(2\sqrt2+\pi)\ \text{in}`

The area of circular segment BCD:

`A_(BCD)=\frac14\cdot \pi R^2 =\frac14\cdot \pi\cdot 8^2 =\frac14\cdot \pi\cdot 64 =16\pi`
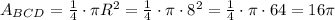III. The area of triangle BCD:

`A_(\Delta BCD)=\frac12\cdot8\cdot8=32`
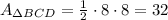IV. The area of figure:

`A=A_(BCD)-A_(\Delta BCD)=16\pi-32=16(\pi-2)\ \text{in}`