Question

"a metal sphere of radius 5.00 cm is initially uncharged. how many electrons would have to be placed on the sphere to produce an electric field of magnitude 1.53 ✕ 105 n/c at a point 8.64 cm from the center of the sphere?"

Answer 1

Outside the radius of the sphere, the electric field generated by a charged sphere (with charge Q on its surface) at a distance r from the centre is equivalent to the electric field generated by a single-point charge with total charge Q:

`E= k_e (Q)/(r^2)`
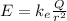
The problem asks to find the electric field at r=8.64 cm, while the radius of the sphere is R=5.00 cm, so r>R and we are exactly in this condition.

Re-arranging the previous formula, we can solve to find the total charge Q on the sphere. Using
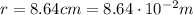
`r=8.64 cm=8.64 \cdot 10^(-2)m` and
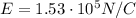
`E=1.53 \cdot 10^5 N/C`, we find

`Q= (Er^2)/(k_e) = ((1.53 \cdot 10^5 N/C)(8.64 \cdot 10^(-2)m)^2)/(8.99 \cdot 10^9 Nm^2C^(-2)) =1.27 \cdot 10^(-7)C`

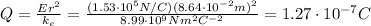
This is the total charge on the surface. If we want to find the number of electrons composing this charge, we should divide the total charge by the charge of a single electron, e:

`N= (Q)/(e) = (1.27 \cdot 10^(-7)C)/(1.6 \cdot 10^(-19)C)=7.9 \cdot 10^(11)`
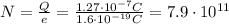
and this is the number of electrons.