Question

A piano tuner stretches a steel piano wire with a tension of 1000 n. the wire is 0.5 m long and has a mass of 5 g. what is the number of the highest harmonic that could be recorded by a computer that is capable of sensing frequencies up to 10,000 hz

Answer 1

Answer: 1. B) 720 N

2. D) 2500 m

3. D) 408 Hz

4. C) 4m

5. A) 246 hz

6. D) 31st

7. B) the frequency of the sound is 100 Hz

8. C) 0.78 m

9. B) 16 Hz

10. B) 311 m/s

Answer 2

The frequencies of the n-harmonics of a string is given by

`f_n = (n)/(2L) \sqrt{ (T)/(\mu) }`
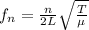
where n is the number of the harmonic, L the length of the wire, T the tension and
`\mu = (m)/(L)` is the linear density, with m being the mass of the string.
Let's calculate the linear density first, using the mass
`m=5 g=5 \cdot 10^(-3)kg`:

`\mu = (m)/(L) = (5\cdot 10^-3 kg)/(0.5 m)=0.01 kg/m`
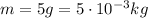
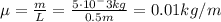
The problem says that the computer is able to analyze frequencies up to 10000 Hz. This means that we have to find the highest number of harmonic that generates a frequency smaller than this value. So, using
`f=10000 Hz`, the tension of the string
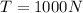
`T=1000 N` and the mass m and the length of the string L, we can re-arrange the previous formula to find which n corresponds to this frequency:

`n = 2f_n L \sqrt{ (\mu)/(T) }=2 (10000 Hz)(0.5 m) \sqrt{ (0.01 kg/m)/(1000 N) }=31.6`
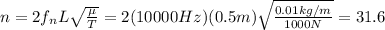
And since n can only be integer, the highest harmonic that can be analyzed by the computer is n=31.