Question

"(a) how much charge can be placed on a capacitor with air between the plates before it breaks down if the area of each plate is 6.00 cm2? (assume air has a dielectric strength of 3.00 ✕ 106 v/m and dielectric constant of 1.00.)"

Answer 1

The voltage value for the electric breakdown is given by

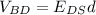
`V_(BD)=E_(DS) d` (1)
where
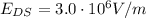
`E_(DS)=3.0 \cdot 10^6 V/m` is the dielectric strenght of the air while d is the distance between the two plates of the capacitor.

For a parallel plate capacitor, the capacitance is given by

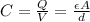
`C= (Q)/(V)= (\epsilon A)/(d)` (2)
where Q is the charge on the capacitor, V the voltage applied,
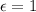
`\epsilon=1` is the dielectric constant in air and
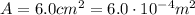
`A=6.0 cm^2 = 6.0 \cdot 10^(-4) m^2` is the area of the plates in our problem.

If we use the breakdown voltage given by equation (1) and replace V in equation (2) with this value, we find:

`(Q)/(E_(DS) d)= (\epsilon A)/(d)`
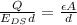
and from this, we can find the maximum charge allowed on the capacitor before the break down:

`Q=\epsilon A E_(DS)= (1)(6\cdot 10^(-4)m^2)(3 \cdot 10^6 V/m)=1800 C`