Question

A 5.00-a current runs through a 12-gauge copper wire (diameter 2.05 mm) and through a light bulb. copper has 8.5 * 1028 free electrons per cubic meter. (a) how many electrons pass through the light bulb each second

Answer 1

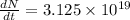`(dN)/(dt) = 3.125 * 10^(19)` electrons per second

Step-by-step explanation:

As we know that electric current is defined as rate of flow of electric charge

so here we will have

`i = (dq)/(dt)`

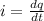
here we know that

`q = Ne`

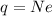
now from above equation

`i = e(dN)/(dt)`

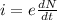
here we know

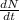`(dN)/(dt)` = number of electrons passing per second

e = charge of an electron

i = 5.00 Ampere

now from above equation we have

`(dN)/(dt) = (i)/(e)`

`(dN)/(dt) = (5)/(1.6 * 10^(-19))`

`(dN)/(dt) = 3.125 * 10^(19)`

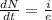
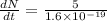
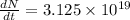
so above is the total number of electrons passing through wire per second

Answer 2

The correct answer is:
`3.125*10^(19)` electrons/second

Step-by-step explanation:

5A current is passing through the copper wire and the light bulb; it means that 5 Coulombs of charge per second is passing through the wire (as current = coulombs/second). To find the electrons per second, the following formula is used:

Electrons per second =
`n_e=(5)/(e)=(5)/( 1.60\cdot 10^(-19))=3.125*10^(19)`