Question

Use the Product Rule to find the derivative of :

a.
`y=(3x-1)^3(2x+5)`

b.
`y=(3x-2)(2x^2+3)`

Answer 1

see explanation

Explanation:

Using the product rule

Given

y = f(x)g(x) , then

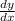`(dy)/(dx)` = f(x).g'(x) + g(x).f'(x) ← product rule

(a)

let

f(x) = (3x - 1)³ , then using the chain rule

f'(x) = 3(3x - 1)² ×
`(d)/(dx)`(3x - 1) = 3(3x - 1)² × 3 = 9(3x - 1)²

let

g(x) = 2x + 5 ⇒ g'(x) = 2

Then

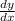`(dy)/(dx)` = (3x - 1)³ . 2 + (2x + 5) × 9(3x - 1)²

= 2(3x - 1)³ +9(3x - 1)²(2x + 5) ← factor out (3x - 1)²

= (3x - 1)²[ 2(3x - 1) + 9(2x + 5) ]

= (3x - 1)² [ 6x - 2 + 18x + 45 ]

= (3x - 1)²(24x + 43)

--------------------------------------------------------------

(b)

let

f(x) = 3x - 2 ⇒ f'(x) = 3

let

g(x) = 2x² + 3 ⇒ g'(x) = 4x

Then

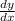`(dy)/(dx)` = (3x - 2).4x + (2x² + 3). 3 ← distribute parenthesis

= 12x² - 8x + 6x² + 9

= 12x² - 8x + 9

Note

It is usual to simplify after differentiating the expressions