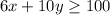Answer:
Let x represent the number of small boxes.
Let y represent the number of large boxes.
The client receive no more than 8 of the large boxes and no fewer than 6 of the small boxes.
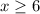
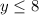
The cost of small box is $4 and the cost to the client for a large box is $6. The client does not wish to exceed $200.
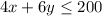
The small box contains 6 of the toy and the large box contains 10 of the toy. A client orders no fewer than 100 of the toy.