Question

Y = 2/3 x -3 y = -3/2 x +2 what statement about the lines are true

Answer 1

The product of the slopes of lines is -1.

i.e. m₁ × m₂ = -1

Thus, the lines are perpendicular.

Explanation:

The slope-intercept form of the line equation

`y = mx+b`

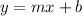
where

• m is the slope

• b is the y-intercept

Given the lines

y = 2/3 x -3 --- Line 1

y = -3/2x +2 --- Line 2

The slope of line 1

y = 2/3 x -3 --- Line 1

By comparing with the slope-intercept form of the line equation

The slope of line 1 is: m₁ = 2/3

The slope of line 2

y = -3/2x +2 --- Line 2

By comparing with the slope-intercept y = mx+b form of the line equation

The slope of line 2 is: m₂ = -3/2

We know that when two lines are perpendicular, the product of their slopes is -1.

Let us check the product of two slopes m₁ and m₂

m₁ × m₂ = (2/3)(-3/2 )

m₁ × m₂ = -1

Thus, the product of the slopes of lines is -1.

i.e. m₁ × m₂ = -1

Thus, the lines are perpendicular.