Question

The question is in the image below.

Answer 1

The Recursive Formula for the sequence is:

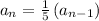`\:a_n=(1)/(5)\left(a_(n-1)\right)` ; a₁ = 125

Hence, option D is correct.

Explanation:

We know that a geometric sequence has a constant ratio 'r'.

The formula for the nth term of the geometric sequence is

`a_n=a_1\cdot r^(n-1)`

where

aₙ is the nth term of the sequence

a₁ is the first term of the sequence

r is the common ratio

We are given the explicit formula for the geometric sequence such as:

`a_n=125\left((1)/(5)\right)^(n-1)`

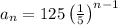
comparing with the nth term of the sequence, we get

a₁ = 125

r = 1/5

Recursive Formula:

We already know that

• a₁ = 125

• r = 1/5

We know that each successive term in the geometric sequence is 'r' times the previous term where 'r' is the common ratio.

i.e.

`a_n=ra_(n-1)`

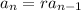
Thus, substituting r = 1/5

`\:a_n=(1)/(5)\left(a_(n-1)\right)`

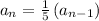
and a₁ = 125.

Therefore, the Recursive Formula for the sequence is:

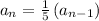`\:a_n=(1)/(5)\left(a_(n-1)\right)` ; a₁ = 125

Hence, option D is correct.