To find the area of the cylinder we need to find its volume first. Remember that the formula for the volume of a cylinder is
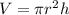
where:
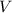
is the volume

is the radius
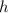
is the height
From the question we know that
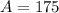
and
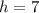
. Lets replace those values in our volume formula:
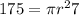
Now we can solve for

to find our radius:
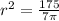
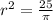
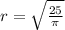
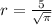
Now that we know the radius, we can use the formula for the area of a cylinder
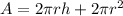
where:
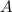
is the area

is the radius
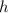
is the height
We know now that
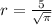
and
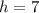
, so lets replace those values in our area formula:
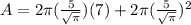
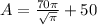
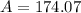
We can conclude that the area of a cylinder that has a volume of 175 cubic units and a height of 7 units is
174.07 square units.