Question

A person invests 9000 dollars in a bank. The bank pays 4.75% interest compounded quarterly. To the nearest tenth of a year, how long must the person leave the money in the bank until it reaches 12600 dollars?

A=P(1+nr)nt

Answer 1

The time required to get a total amount of $ 12,600.00 from compound interest on a principal of $9000 at an interest rate of 4.75% per year and compounded 4 times per year is 7.1 years.

Explanation:

Given

Principle P = 9000 dollars

Rate r = 4.75% = 0.0475

Total Amount A = 12600 dollars

compounded quarterly n = 4

To determine:

Time t = ?

Using the equation

`A\:=\:P\left(1\:+\:(r)/(n)\right)^(nt)`

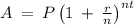
solving the equation for 't'

t = ln(A/P) / n[ln(1 + r/n)]

t = ln(12,600.00/9,000.00) / ( 4 × [ln(1 + 0.011875/4)] )

t = 7.1 years

Therefore, the time required to get a total amount of $ 12,600.00 from compound interest on a principal of $9000 at an interest rate of 4.75% per year and compounded 4 times per year is 7.1 years.