Question

Consider the function y = 9 - x2, where x ≥ 3. What is the inverse of the function? What is the domain of the inverse? Show all of your work for full credit.

Answer 1

Hello,
Please see the attached file.
Thanks.

Answer 2

The inverse of the function is
`y^(-1)=√(9-x)`.

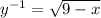The domain of the inverse function is
`D:(-\infty,0],\{x|x\in \mathbb{R}\}`

Explanation:

Given : Function
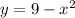`y=9-x^2` where,
`x\geq 3`

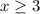
To find : What is the inverse of the function? What is the domain of the inverse?

Solution :

Function
`y=9-x^2`

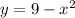
To find the inverse we interchange the value of x and y,

`x=9-y^2`

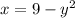
Now, we get the value of y

`y^2=9-x`

`y=\pm√(9-x)`

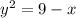
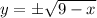
As
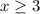`x\geq 3` so x>0

`y=√(9-x)`

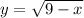
The inverse of the function is
`y^(-1)=√(9-x)`.

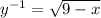The domain of the inverse is the range of the original function.

The range is defined as the set of all possible value of y.

As
`x\geq 3`

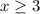
Squaring both side,

`x^2\geq 9`

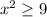
Subtract
`x^2` both side,

`9-x^2\leq 0`

`y\leq 0`

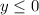
The range of the function is
`R:(-\infty,0],\{y|y\in \mathbb{R}\}`

The domain of the inverse function is
`D:(-\infty,0],\{x|x\in \mathbb{R}\}`