Question

At noon, ship a is 60 km west of ship

b. ship a is sailing south at 15 km/h and ship b is sailing north at 5 km/h. how fast is the distance between the ships changing at 4:00 pm?

Answer 1

dA/dt=15 km/h and dB/dt=5 km/h
base of our triangle if drawn is 60 km
to find dD/dt when t=4 hours we shall have:

(A+B)²+60²=D²
d/dt[(A+B)²+60²]=d/dt(D²)
[d(A+B)]/dt*2(A+B)(2)=dD/dt*2D
B=5km/h*4hr=20km
A=15km/hr*4=60km
20²+60²=D²
D=√4000

(15+5)*(2)*80*(2)=2*√4000*dD/dt
dD/dt=6400/√4000=101.192 km/hr

Answer 2

The two ships are sailing in opposite sides, Hence, the resultant speed is given by 15+5 = 20 km/hr.

Therefore, from the below triangle, we have

`(dx)/(dt) = 20 \text{  km/hr}`

Let the distance between the ships is y. On applying Pythagorous theorem, we have

`y^2=x^2+60^2\\ \text{On differentiating, we get}\\ 2y(dy)/(dt) =2x(dx)/(dt)\\(dy)/(dt)= (x)/(y) (dx)/(dt)`

On substituting the value of y as
`y=√(60^2+x^2)`

`(dy)/(dt) =(x)/(√(60^2+x^2)) (dx)/(dt)`

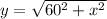
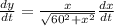
Since, the at noon the ship is 60 km to each other. Hence, for 4 PM, i.e. t=4, we have

`x=4 * (dx)/(dt) \\ x= 4 * 20 \\x=80`

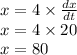
On substituting the value in above, we get

`(dy)/(dt) =(80)/(√(60^2+80^2)) (20`

`(dy)/(dt) = 16.0 \text{ km/hr}`

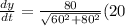
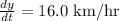
Therefore, the distance between the ships changing at a rate of 16 km/hr at 4:00 pm