Question

If three tangents to a circle form an equilateral triangle, prove that the tangent points form an equilateral triangle inscribed in the circle

Answer 1

I added a figure so you can guide yourself throughout the proof I'm about to write, so I recommend that you download the picture beforehand and have this window and the picture's window open. Alright, let's get started!
Assuming that
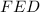
`FED` is an equilateral triangle according to the wording of the problem, we have that the angles
`\widehat{AFB}=\widehat{BEC}=\widehat{CDA}=60`.
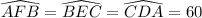
We also know that the circle in green is Inscribed in
`FED`.

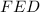
The following applies to every inscribed circle inside a triangle:
The center of the inscribed circle of a triangle is the intercept of all three angle bisectors of the triangle.

The above theorem implies that the line
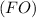
`(FO)` is an angle bisector because it goes through the vertex F and the center of the inscribed circle.

The previous statement implies that the angle
`\widehat{OFB}=30`.

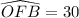
Now let's work on the
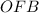
`OFB` triangle.
Knowing that
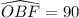`\widehat{OBF}=90` (because
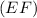`(EF)` is tangent to the circle at B and
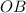`OB` is a radius of the circle. If you're lost here, remember that a tangent to a circle is always perpendicular to the radius of the circle.) we can then derive that
`\widehat{FOB}=180-90-30=60` (because the sum of the measures of all angles in a triangle is always equal to 180 degrees).

In the same way, we can prove also that:

`\widehat{BOE}=\widehat{EOC}=\widehat{COD}=\widehat{DOA}=\widehat{AOF}=60 degrees`.
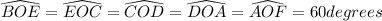
Knowing the above we notice that
`\widehat{BOC}=\widehat{COA}=\widehat{AOB}=120degrees`.

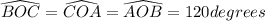
We're at the last part of our proof here:
Now notice that
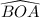
`\widehat{BOA}` subtends the same arc on the circle that
`\widehat{BCA}`.
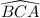
According to the inscribed angle theorem, an angle
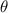
`\theta` inscribed in a circle is half of the central angle
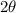
`2\theta` that subtends the same arc on the circle.
Therefore
`\widehat{BCA}=\frac{\widehat{BOA}}{2}=60degrees`

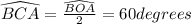
We can prove in a similar fashion that:
`\widehat{CAB}=\widehat{ABC}=60degrees`
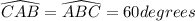
Therefore all the angles of the
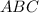
`ABC` triangle have a measure of 60 degrees, we conclude then that
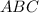
`ABC` is equilateral.