Question

The profits of mr cash’s company is represented by the equation p(t)=-3t^2+18t-4, where p(t) is the amount of profit in hundreds of thousands of dollars and t is the number of years of operation. he realizes his company is on the down turn and wishes to sell before he ends up in debt. in what year of operation does mr cash’s business show the maximum profit?

Answer 1

Answer: 3rd year of operation

Step-by-step explanation:

Note that p(t) is a quadratic function and so its graph is a parabola. Since the coefficient of t² in p(t) is negative, the maximum point in p(t) exist at its vertex. Moreover, the maximum value of p(t) is the y-coordinate of its vertex.

Note that p(t) can be expressed as:


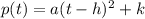
`p(t) = a(t-h)^2 + k` (1)

Where (h, k) are the coordinates of the vertex of p(t).

To manipulate p(t) in the form expressed in equation (1), we factor out the coefficient of t² in p(t) so that


`p(t) = -3t^2+18t-4 \\ \boxed{p(t) = -3 \left( t^2 - 6t + (4)/(3) \right)}`

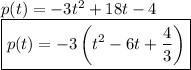
Then, we let


`q(t) = t^2 - 6t + (4)/(3)`

So that


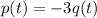
`p(t) = -3q(t)` (2)

We need q(t) to be expressed as the sum of a perfect square trinomial and a constant. To form the perfect square trinomial in q(t), we can find a constant k such that
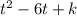
`t^2 - 6t + k` is a perfect square.

To find the value of k, we divide the coefficient of t by 2 and get the square of the result. Since the coefficient of t in q(t) is -6,


`k = \left( (-6)/(2) \right)^2 = 9`

To avoid changing the value of q(t), if we add the constant k = 9, we need to subtract it by the same number. Since k = 9,


`q(t) = t^2 - 6t + (4)/(3) + k - k \\ = t^2 - 6t + (4)/(3) + 9 - 9 \\ = (t^2 - 6t + 9) + (4)/(3) - 9 \\ \boxed{q(t) = (t - 3)^2 - (23)/(3)}`

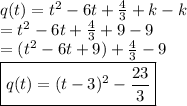
From equation (2),


`p(t) = -3q(t) \\ p(t) = -3\left( (t - 3)^2 - (23)/(3) \right) \\ \boxed{p(t) = -3 (t - 3)^2 + 23}`

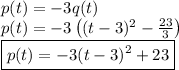
Hence the vertex of p(t) is (3, 23) and maximum value is attained at t = 3. Therefore, the Mr. Cash's business has maximum profit at the 3rd year of operation.