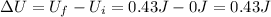Question

A spring with a spring constant k of 44 n/m is stretched a distance of 14 cm (0.14 m) from its original unstretched position. what is the increase in potential energy of the spring? j

Answer 1

The elastic potential energy of a spring is given by

`U= (1)/(2) k x^2`
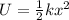
where k is the spring's constant and x is the displacement with respect to its unstretched position.

The initial potential energy of the spring is zero, because it is in unstretched postion, therefore x=0. The final potential energy is instead, using
`k=44 N/m` and
`x=0.14 m`,

`U_f = (1)/(2) (44 N/m)(0.14 m)^2 = 0.43 J`

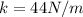
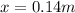
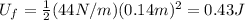
And so, the increase in potential energy is

`\Delta U=U_f - U_i = 0.43 J-0 J=0.43 J`