Question

An electron is released from rest and travels over a potential difference of 2500 v. what is its final velocity?

Answer 1

The electron travels through a potential difference of
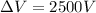
`\Delta V =2500 V`. This means that the loss of electrostatic potential energy of the electron is

`\Delta U = q \Delta V= (-1.6 \cdot 10^(-19)C)(2500 V)=-4 \cdot 10^(-16)J`
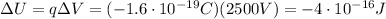
where q is the electron charge.

For the law of conservation of energy, the electron (starting from rest and accelerated by the potential difference) acquired a kinetic energy equal to the negative of this loss of potential energy:

`\Delta K=-\Delta U`
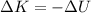
where
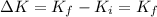
`\Delta K =K_f - K_i = K_f` because the electron is initially at rest and so its kinetic energy is zero. Since

`K_f= (1)/(2)mv^2`
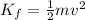
where m is the electron mass, we can find the final velocity v of the electron:

`v= \sqrt{ (2K_f)/(m) }= \sqrt{ (2\cdot 4 \cdot 10^(-16) J)/(9.1 \cdot 10^(-31) kg) }=3.0 \cdot 10^7 m/s`