Question

In a distribution, a score of X=60 has a z-score of -3.0.. A score of X=85 has a z-score of 2.0. What are the mean and standard deviation for this population?

Answer 1

The formula for a z-score is

`z=(X- \mu)/(\sigma)`
We don't have μ, the mean, or σ, the standard deviation. We can, however, set up a system of two equations with the information we do have. We know:

`-3=(60- \mu)/(\sigma) \text{ and } 2=(85- \mu)/(\sigma)`
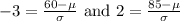
We can make this look more like a "typical" system of equations by cancelling the fractional part of each equation. We do this by multiplying the bottom of each equation by σ:

`-3*\sigma=(60- \mu)/(\sigma)*\sigma \text{ and } 2*\sigma=(85- \mu)/(\sigma)*\sigma \\ \\-3\sigma=60- \mu \text{ and } 2\sigma=85- \mu`
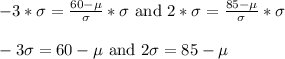
Now we'll get the variables on the same side of the equation. We'll do this by adding μ to both sides:

`-3\sigma + \mu=60- \mu + \mu \text{ and } 2\sigma+ \mu =85- \mu + \mu \\ \\-3\sigma+\mu=60 \text{ and } 2\sigma+\mu=85`
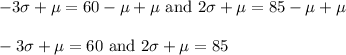
Now we'll write this vertically:

`\left \{ {{-3\sigma+\mu=60} \atop {2\sigma+\mu=85}} \right.`
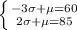
We will "eliminate" μ by subtracting the bottom equation:

`\left \{ {{-3\sigma+\mu=60} \atop {-(2\sigma+\mu=85)}} \right. \\ \\-5\sigma=-25`
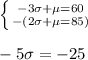
Divide both sides by -5:

`(-5\sigma)/(-5)=(-25)/(-5) \\ \\\sigma=5`
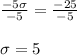
Our standard deviation is 5. Substituting this into our top equation we have:
-3(5)+μ=60
-15+μ=60
Cancel the -15 by adding it to both sides:
-15+μ+15=60+15
μ=75
Our mean is 75.