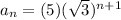Part 1.] Indicate the general rule for the arithmetic sequence with
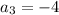
and
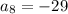
A.]
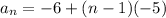
B.]
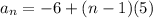
C.]
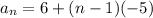
D.]
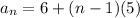
Part 2.] Which of the following is the general term for the sequence m, -m, m, -m, . . .?
A.]
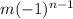
B.]
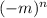
C.]
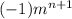
D.]
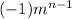
Part 3.] Indicate a general rule for the
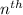
term of the sequence when
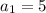
and

A.]
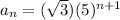
B.]
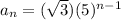
C.]
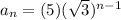
D.]