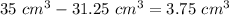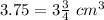Answer:
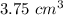 or
or
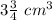
Explanation:
step 1
Find the volume of the rectangular prism
we know that
The volume of a rectangular prism is
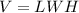
In this problem we have
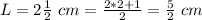
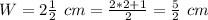
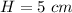
substitute in the formula
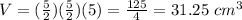
step 2
Find the difference between the volume of the prism and the volume of the storage container