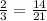Question

How can a ratio's number can be changed without changing the ratio itself

Answer 1

The ratio is a fraction that tells us how many times longer a thing is compared to another thing. In mathematics, we express a ratio as the relationship between two numbers, namely
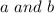`a \ and \ b`, so the ratio can be written as:

`r=(a)/(b)`

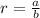
If we can change this number without changing the ration we need to multiply both the numerator and the denominator by the same number. For instance, if we have the following ratio:

`r=(2)/(3)`

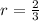
We can multiply both the numerator and denominator, say, by 7. Then:

`r=(7* 2)/(7 * 3)=(14)/(21)`

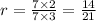
As you can see, the ratio's number has changed but without changing the ratio itself because:

`(2)/(3)=(14)/(21)`