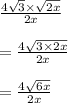Question

NEED HELP ASAP What is the simplified form of the following expression? 4 sqrt 3/2x Assume x>0

Answer 1

The correct answer is ^4sqrt24x^3/2x or B on edge.

Explanation:

Answer 2

`(4√(6x))/(2x)`

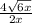
Explanation:

The problem we are given is

`4\sqrt{(3)/(2x)}`

We can write the square root of a fraction as a fraction with a separate radical for the numerator and denominator; this gives us

`4* (√(3))/(√(2x))`

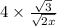
We can write the whole number 4 as the fraction 4/1; this gives us

`(4)/(1)* (√(3))/(√(2x))\\\\=(4√(3))/(√(2x))`

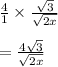
We now need to "rationalize the denominator." This means we need to cancel the square root in the denominator. In order to do this, we multiply both numerator and denominator by √(2x); this is because squaring a square root will cancel it:

`(4√(3))/(√(2x))* (√(2x))/(√(2x))\\\\=(4√(3)* √(2x))/(2x)`

When multiplying radicals, we can extend the radical over both factors:

`(4√(3) * √(2x))/(2x)\\\\=(4√(3* 2x))/(2x)\\\\=(4√(6x))/(2x)`