Question

five cards are drawn from a standard deck of cards. each card is replaced after being drawn. what is the probability of the following event: p(3 and 3 and 3 and 2 and 2)?

Answer 1

the probability of the next card being 3 is a 4/5 chance

Answer 2

General Idea:

If A and B are independent, then the probability that events A and B both occur is:

`p(A\; and\; B) = p(A) * p(B).`

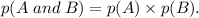
In other words, the probability of A and B both occurring is the product of the probability of A and the probability of B

Applying the concept:

Five cards are drawn from a standard deck of cards. Each card is replaced after being drawn.

There are four 3's in a deck of card, four 2's in a deck of card. In a deck of card there are 52, so...

`\\[tex] p(3\; and\; 3\; and\; 3 \; and \; 2 \; and\; 2)=(4)/(52) * (4)/(52) * (4)/(52) * (4)/(52) * (4)/(52) \\ \\ Multiply \; numerator \; with \; numerator \; and \; denominator \; with \; denominator\\ \\ (4 \cdot 4 \cdot 4 \cdot 4 \cdot 4)/(52 \cdot 52 \cdot 52 \cdot 52 \cdot 52) \\ \\ Cancel \; Common\; Factor\\ \\ (1 \cdot 1 \cdot 1 \cdot 1 \cdot 1)/(13 \cdot 13 \cdot 13 \cdot 13 \cdot 13) =(1)/(13^5) =(1)/(371293)` \; =\; p(3) \times \; p(3) \times \; p(3) \times \; p(2) \times p(2) [/tex]