Question

Jimmy invest $16,000 in an account that pays 7.03% compounded quarterly. How long (in years and months) will it take for his investment to reach $23,000?

Answer 1

To solve this we are going to use the compound interest formula
`A=P(1+ (r)/(n))^(nt)`
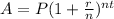
where:

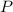
`P` is the investment

`r` is the interest rate in decimal form

`n` is the number of times the interest is compounded per year

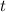
`t` is the time in years

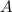
`A` is the amount after
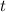
`t` years

First, lets convert the interest rate to decimal dividing it by 100%:

`r= (7.03)/(100) =0.0703`
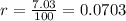
Next, lets find
`n`. Since we know that the interest is compounded every 4 months (quarterly), it will be compounded
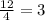
`(12)/(4) =3` times in a year, so
`n=4`.
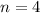
We also know that
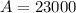
`A=23000` and
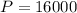
`P=16000`, so lets replace all the quantities into our compound interest formula:

`25000=16000(1+ (0.0703)/(3))^(3t)`

`25000=16000(1.0234)^(3t)`

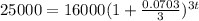
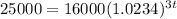
Notice that the the number of years
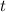
`t` is in the exponent, so we have to use logarithms to bring it down. But first lets divide both sides by 16000 to isolate the exponential expression:

`(25000)/(16000) =(1.0234)^(3t)`

`(1.0234)^(3t) = (25)/(16)`

`ln(1.0234)^(3t) =ln( (25)/(16) )`

`t= (ln( (25)/(16)) )/(3ln(1.0234))`

`t=6.43`

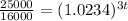
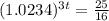
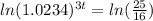
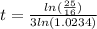
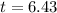
Now that we know
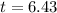
`t=6.43`, the last thing to do is convert 0.43 years to months:

`(0.43 years)( (12months)/(1year) )=5.16months`

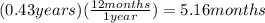
We can conclude that Jimmy's investment will take 6 years and 5 months to reach $25,000.