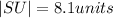ANSWER
The correct answer is C.
Step-by-step explanation
The given points are,
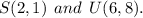
We use the distance formula to determine the distance between the two points.
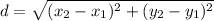
We substitute the points to obtain,
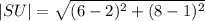
We simplify to obtain,
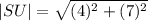
We further simplify this to obtain,
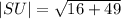
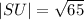
This evaluates to,
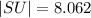
We round to the nearest tenth to get,