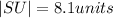Question

What is the distance between points S and U?

Round to the nearest tenth of a unit.

3.3 units
6.4 units
8.1 units
12.0 units

Answer 1

ANSWER

The correct answer is C.


`|SU| = 8.1units`


Step-by-step explanation

The given points are,

`S(2,1) \: \: and \: \: U(6,8).`


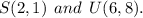
We use the distance formula to determine the distance between the two points.




`d = √((x_2-x_1)^2+(y_2-y_1)^2)`


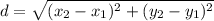
We substitute the points to obtain,


`|SU| = \sqrt{(6- 2) ^(2) + (8 - 1) ^(2) }`

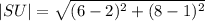
We simplify to obtain,


`|SU| = \sqrt{(4) ^(2) + (7) ^(2) }`



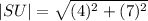
We further simplify this to obtain,


`|SU| = √(16 + 49)`




`|SU| = √(65)`

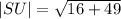
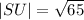
This evaluates to,


`|SU| = 8.062`



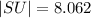
We round to the nearest tenth to get,


`|SU| = 8.1units`

Answer 2

distance = sqrt((6-2)^2 +(8-1)^2)
sqrt(16 +49)
sqrt(65)
8.06
round to 8.1 units