Question

Formulate the recursive formula for the following geometric sequence.
{-16, 4, -1, ...}

Answer 1

`a_(n) =(-a_(n-1))/(4)`.

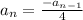Explanation:

We are given a geometric sequence { -16, 4, -1, .... }

i.e.
`a_(1) =-16`,
`a_(2) =4`,
`a_(3) =-1`, ...

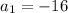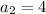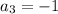We will first find the common ratio 'r'.

Now,
`r=(a_(n))/(a_(n-1))`

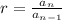
i.e.
`r=(a_(2))/(a_(1))`

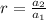
i.e.
`r=(4)/(-16)`

i.e.
`r=(1)/(-4)`

Similarly, i.e.
`r=(a_(3))/(a_(2))`

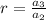
i.e.
`r=(-1)/(4)`

So, we get that the common ratio is
`r=(-1)/(4)`.

Now, the recursive formula for the geometric sequence is given by,

`a_(n) =r * a_(n-1)`

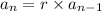
i.e.
`a_(n) =(-1)/(4) * a_(n-1)`

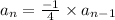
i.e.
`a_(n) =(-a_(n-1))/(4)`.

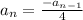Hence, the recursive formula for this sequence is
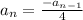`a_(n) =(-a_(n-1))/(4)`.