Question

Match the reasons with the statements in the proof.

1. j||k, m∠3 = m∠1
If alternate interior angles are =, then lines are ||.
2. m∠1 = m∠2
Substitution
3. m∠2 = m∠3
Given
4. l||m
If lines are ||, then corresponding angles are =.

Answer 1

1. j||k, m∠3 = m∠1
Given

2. m∠1 = m∠2
If lines are ||, then corresponding angles are =.


3. m∠2 = m∠3
Substitution

4. l||m
If alternate interior angles are =, then lines are ||.

Answer 2

1-given

2-if lines are parallel, then corresponding angles are equal

3-Substitution

4-if alternate interior angles are equal then lines are parallel.

Explanation:

Given j is parallel to k,
`m\angle3 =m\angle 1`

We have to prove that line l is parallel to m

We have to match reason with its correct statement in given proof.

1.j is parallel to k,
`m\angle 3=m\angle 1`

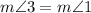
Reason:given

2.
`m\angle 1=m\angle 2`

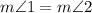
Reason:if the lines are parallel , then corresponding angles are equal.

3.
`m\angle 2=m\angle 3`

Reason: substitution

4.line l is parallel to m

Reason: If alternate interior angles are equal ,then lines are parallel.