Use Lagrange multipliers. The Lagrangian is
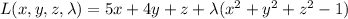
with partial derivatives (set equal to 0)
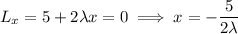
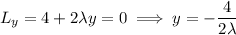
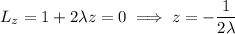
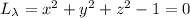
We can substitute the first three equations into the fourth to solve for
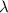
:
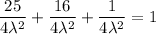
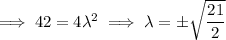
Now use these values of
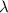
to solve for
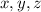
, which should give you two critical points at
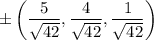
, which would respectively give a maximum and minimum value of
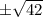
.