Question

Find the maximum and minimum values of f(x,y,z)=5x+4y+1z on the sphere x2+y2+z2=1.

Answer 1

Use Lagrange multipliers. The Lagrangian is


`L(x,y,z,\lambda)=5x+4y+z+\lambda(x^2+y^2+z^2-1)`

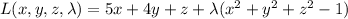
with partial derivatives (set equal to 0)


`L_x=5+2\lambda x=0\implies x=-\frac5{2\lambda}`

`L_y=4+2\lambda y=0\implies y=-\frac4{2\lambda}`

`L_z=1+2\lambda z=0\implies z=-\frac1{2\lambda}`

`L_\lambda=x^2+y^2+z^2-1=0`

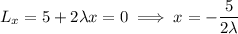
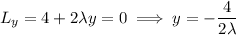
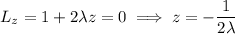
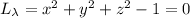
We can substitute the first three equations into the fourth to solve for
`\lambda`:


`(25)/(4\lambda^2)+(16)/(4\lambda^2)+\frac1{4\lambda^2}=1`

`\implies 42=4\lambda^2\implies\lambda=\pm\sqrt{\frac{21}2}`

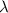
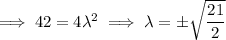
Now use these values of
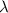
`\lambda` to solve for
`x,y,z`, which should give you two critical points at
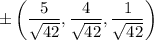
`\pm\left(\frac5{√(42)},\frac4{√(42)},\frac1{√(42)}\right)`, which would respectively give a maximum and minimum value of
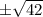
`\pm√(42)`.