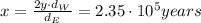First, we need the distance of Europe and Wolf-359 from Earth.
- The distance of Europe from Earth is:
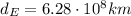
- The distance of Wolf-359 from Earth is instead 7.795 light years. However, we need to convert this number into km. 1 light year is the distance covered by the light in 1 year. Keeping in mind that the speed of light is
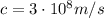
, and that in 1 year there are
365 days x 24 hours x 60 minutes x 60 seconds =
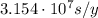
, the distance between Wolf-359 and Earth is
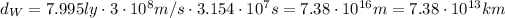
Now we can calculate the time the spaceship needs to go to Wolf-359, by writing a simple proportion. In fact, we know that the spaceship takes 2 years to cover
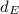
, so
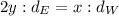
from which we find

, the time needed to reach Wolf-359: