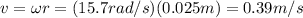Question

A 0.025m radius toy top is spinning at a rate of 150rpm, what is the angular velocity? What is the linear velocity of the paint on the outside edge?

Answer 1

a) The angular velocity of the disk is 150 rpm (revolutions per minute). We can convert it into proper units, i.e. radiants per seconds, keeping in mind that:

`1 rev = 2 \pi rad`

`1 min = 60 s`
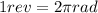
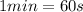
so the angular speed is

`\omega = 150 (rev)/(min) = 150 (2 \pi rad)/(60 s) =15.7 rad /s`

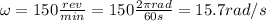
b) The linear velocity is given by

`v=\omega r`
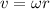
since the radius is r=0.025 m, the linear velocity at the edge of the disk is

`v= \omega r = (15.7 rad/s)(0.025 m)=0.39 m/s`