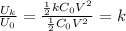The electrostatic energy stored in a capacitor with capacitance
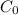
, with a voltage difference V applied to it, and without dielectric, is given by
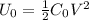
Now let's assume we fill the space between the two plates of the capacitor with a dielectric with constant k. The new capacitance of the capacitor is
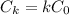
So, the energy stored now is

Therefore, the ratio between the energies stored in the capacitor before and after the introduction of the dielectric is