Question

What's the present value of $11,500 discounted back 5 years if the appropriate interest rate is 4.5%, compounded semiannually?

Answer 1

$1,500/(0.03)^10 = $1,116.14

Answer 2

General Idea:

We need to make use of the below formula to find the present value.

`PV=(FV)/((1+(r)/(n))^(nt)) \\ \\ Where:\\ FV \; is \; Future\; Value\; of \; money\\ r \; is\; Annual\; rate\; of\; interest\\ t\; is\; number\; of\; years\\ n\; is\; Number\; of\; periods\; based\; on\; compounding \; frequency`

Applying the Concept:

We are given the below information:

`FV= \$11,500\\ \\ t=5\; years\\ \\ r=4.5 \%\\ \\ n=2\; (because\; given\; compounded\; semi-annually)`

We need to substitute the above information in the formula to find the Present value.

`PV=(11500)/((1+(0.045)/(2))^(2 * 5)) =(11500)/((1+0.0225)^(10)) =(11500)/(1.0225^(10)) \\ \\ PV \approx \$9206`

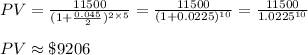
CONCLUSION:

The present value of $11,500 discounted back 5 years if the appropriate interest rate is 4.5%, compounded semiannually is approximately 9206 dollars