Question

The picture below shows a container that Sue uses to freeze water: A cylinder is shown with base diameter of 4 centimeters and the height as 6 centimeters. What is the minimum number of identical containers that Sue would need to make 2,000 cm3 of ice? (Use π = 3.14.) (1 point) 12 18 27 7

Answer 1

Answer: 27

Explanation:

Given: The height of the cylindrical container = 6 cm

Diameter of container = 4 cm

Then the radius of the container =
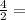`(4)/(2)=`2 cm

Now, the volume of the cylindrical container is given by :-

`\text{Volume}=\pi r^2 h\\\\\Rightarrow\text{Volume}=(3.14)(2)^2(6)=75.3982236862\approx75.4\ cm^3`

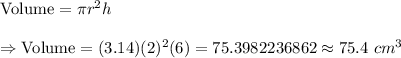
Now, the minimum number of identical containers that Sue would need to make 2,000
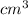`cm^3` of ice is given by:-

`(2000)/(75.4)=26.525198939\approx27`

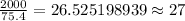
Hence, the minimum number of identical containers that Sue would need to make 2,000
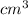`cm^3` of ice is 27.

Answer 2

`27\ containers`

Explanation:

step 1

Find the volume of one container (cylinder) is equal to

`V=\pi r^(2)h`

we have

`r=4/2=2\ cm` -----> the radius is half the diameter

`h=6\ cm`

substitute

`V=(3.14)(2^(2))(6)=75.36\ cm^(3)`

step 2

By proportion

Find the the minimum number of identical containers that Sue would need to make
`2,000\ cm^(3)` of ice

`(1)/(75.36)=(x)/(2,000)\\ \\x=2,000/75.36\\ \\x= 26.5\ containers`

Round to the nearest whole number

`26.5=27\ containers`