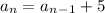Question

The explicit rule for a sequence is

an=17−5n .

What is the recursive rule for the sequence?

can you explain also

Answer 1

`a_(n) = a_(n-1)-5`

`a_(1) = 12`

Explanation:

Answer 2

The general form of an explicit rule for an arithmetic sequence is

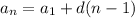
`a_n=a_1+d(n-1)`, where a₁ is the first term of the sequence and d is the common difference. Since we have
`a_n=17-5n`, we know that n is multiplied by 5. That means that d must be 5, since that is the only thing that n gets multiplied in our general form. This gives us:

`a_n=a_1+5(n-1) \\ \\a_n=a_1+5*n-5*1 \\ \\a_n=a_1+5n-5`
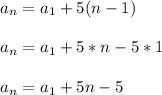
We know that we add something to 5n and then subtract 5 to get 17. Cancelling this process, we can add 5 to 17 to get 22. This gives us

`a_n=22+5(n-1)`
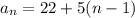
We know that our first term, a₁, is 22 and our common difference, d, is 5.
The general form of a recursive formula for an arithmetic sequence is

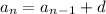
`a_n=a_n_-_1+d`, where d is the common difference and
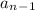
`a_n_-_1` is the previous term. We know that d is 5, so our recursive formula is

`a_n=a_n_-_1+5`