Denote all work that should be done as 1. Then if Cody can complete the project in 8 hours, he can do
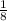 per hour and if Kaitlyn can complete the project in 6 hours, then she can do
per hour and if Kaitlyn can complete the project in 6 hours, then she can do
 per hour. Together they complete
per hour. Together they complete
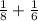 per hour.
per hour.
Simplify this expression:
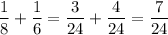 .
.
Then it will take them to complete the project together
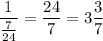 hours
hours
Answer: It will take them to complete the project together
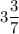 hours.
hours.