Answer:
Explanation:
If the object starts with a value
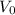 , and a annual percent of decay d, after a year the value will be
, and a annual percent of decay d, after a year the value will be
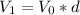
after 2 years, taking now
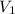 as the starting value
as the starting value
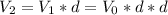
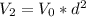
and so on, after n years the value will be:
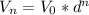
Now, in 1997 the value was $9500, in 2012 the value was $5000. Between 1997 and 2012 there are 15 years, so, our equation will be:
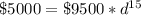
Working it a little
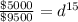
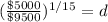
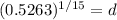
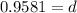
This mean that, after a year, the value will be at 95.81 %, this is, a decay rate of 4.19%.