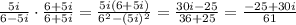Question

Simplify the expression fraction with numerator of the square root of negative twenty five and denominator of the quantity five minus two times i plus the quantity one minus three times i

Answer 1

If I understood you correctly this is the expression we need to simplify:

`(√(-25))/((5-2i)+(1-3i))`
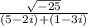
You should keep in mind that square root of -1 is equal to i. i is called the imaginary unit.
Let us simplify this expression:

`(√(-1)\cdot √(25))/(6-5i)= (5i)/(6-5i)`
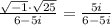
To simplify this further we can multiply numerator and denominator with 6+5i to elimante imaginary numbers from denominator.

`(5i)/(6-5i)\cdot (6+5i)/(6+5i) = (5i(6+5i))/(6^2-(5i)^2)= (30i-25)/(36+25)= (-25+30i)/(61)`