Answer:
Quadratic equation:

Explanation:
We are given two roots of the quadratic equation and we need to find the quadratic equation.
If roots are a and b then equation
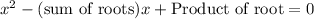
Roots are x=8 and x=-5
Sum of roots = 8 + (- 5) = 3
Product of roots = 8 x -5 = -40
Substitute the value into formula
Quadratic equation:

In factor form:
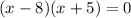
Hence, The equation is
