Question

A sphere has surface area 1.25 m2, emissivity 1.0, and temperature 100.0°C. What is the rate at which it radiates heat into empty space? The Stefan-Boltzmann constant is 5.67 × 10-8 W/(m2 ∙ K4).

A.) 9.9 mW

B.) 3.7 W

C.) 7.1 W

D.) 1.4 kW

Answer 1

The total power emitted by an object via radiation is:

`P=A\epsilon \sigma T^4`
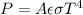
where:
A is the surface of the object (in our problem,
`A=1.25 m^2`

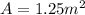
`\epsilon` is the emissivity of the object (in our problem,
`\epsilon=1`)

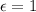
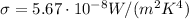
`\sigma = 5.67 \cdot 10^(-8) W/(m^2 K^4)` is the Stefan-Boltzmann constant
T is the absolute temperature of the object, which in our case is
`T=100^(\circ) C=373 K`

Substituting these values, we find the power emitted by radiation:

`P=(1.25 m^2)(1.0)(5.67 \cdot 10^(-8)W/(m^2K^4)})(373 K)^4=1371 W = 1.4 kW`
So, the correct answer is D.